Das Transportproblem in der Betriebswirtschaftslehre

Problemformulierung

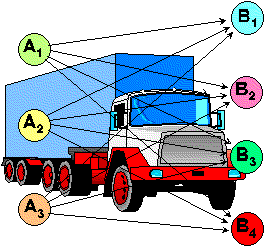
Allgemein formuliert lautet das Transportproblem: Ein homogenes Gut, das an den Orten Ai (i=1,...,m) in den Mengen ai angeboten wird, soll zu den Orten Bj (j=1,...,n) transportiert werden, an denen eine Nachfrage von bj besteht. Die Kosten des Transportes einer Mengeneinheit (ME) von Ort Ai zum Ort Bj betragen cij. Wieviele ME sollen vom Ort Ai zum Ort Bj transportiert werden, so dass die Nachfrage erfüllt wird und die Gesamttransportkosten minimal sind ?

Ohne Einschränkung der Allgemeinheit kann man annehmen, dass eine Transportverbindung von jedem Ort Ai zu jedem Ort Bj existiert. Soll auf einer Verbindung auf keinen Fall ein Transport stattfinden (was gleichbedeutend mit dem Fehlen der Verbindung ist), so erreicht man dies durch die Definition unendlich hoher Transportkosten.

Das Problem der Transportkostenminimierung wird in dieser Form allgemein als das klassische Transportproblem bezeichnet. Das Adjektiv klassisch hat angesichts der historischen Bedeutung dieses Problems durchaus seine Berechtigung, denn die Formulierung als mathematisches Modell und seine Analyse mit Hilfe mathematischer Verfahren kann man als eine der ersten OR-Studien überhaupt ansehen. DANTZIG (1966), der selbst maßgeblich Anteil an der Behandlung der Transportprobleme hatte, skizziert die Meilensteine dieser Entwicklung.

• Die erste Formulierung stammt von KANTOROWICH (1939).
• Das erste Lösungsverfahren, die sog. MODI(=Modified Distribution)-Methode, wird von DANTZIG 1951 entwickelt.
• Auf der primalen Simplex-Methode basiert die sog. Stepping-Stone-Methode von CHARNES und COOPER (1954).
• Es werden Eröffnungsverfahren zur Bestimmung einer zulässigen Ausgangslösung, wie z.B. die sogenannte Nord-West-Ecken-Methode oder die Matrix-Minimum-Methode entwickelt.
• FORD und FULKERSON (1957) interpretieren das Transportproblem als Flussproblem und lösen es mit Hilfe von Flussmaximierungsverfahren.

JavaScript-Applikation zum »Transportproblem«

Die Verteilung leerer Güterwaggons stellt ein aus betriebswirtschaftlicher Sicht interessantes Optimierungsproblem dar, nicht zuletzt weil jede Bahngesellschaft daran interessiert sein muss, die Anzahl der Leerfahrten zu minimieren.
Formuliert man die Aufgabe als Transportproblem mit m Ausgangs- und n Zielorten, wobei die »Anbieter« A_i am Abend eines Tages eine Anzahl von Waggons in ihren Bahnhöfen stehen habe, die am nachfolgenden Tag von den »Nachfragern« B_j benötigt werden. Die Waggons müssen im sogenannten Nachtsprung verschoben werden. Hauptziel ist die Deckung aller Bedarfe und damit die maximale Zufriedenheit der Kunden.
Für eine konkrete Fragestellung zu den Güterbahnhöfen von Darmstadt, Mainz, München, Saarbrücken, Essen, Bremen, Hamburg und Lübeck kann mit einer JS-Applikation dieses Problem experimentell mit verschiedenen, im Kurs 000852-KE2 vorgestellten Algorithmen gelöst werden.
Literatur

• Jandy, G.: Optimale Transport- und Verkehrsplanung, (Physica, Würzburg, 1967).
• Rechnergesteuerte Leerwagenverteilung (LWV), zahlreiche Beiträge verschiedener Verfasser, Die Bundesbahn 67-4 (1991) 389-431.