Die Nutzung von SciLab für Algorithmen der Graphentheorie
Einführung
Scilab ist ein frei verfügbares Softarepaket zur Lösung mathematischer Problemstellungen. Zum Funktionsumfang von Scilab gehören Methoden zur linearen Algebra, Analysis und Statistik. Ebenfalls verfügbar ist eine Bibliothek zur Graphentheorie und zur Simulation. Neben den vordefinierten Funktionen bietet Scilab mittels einer Skriptsprache die Möglichkeit eigene Funktionen zu implementieren und durch Schnittstellen C- und MATLab Routinen einzubinden. Eine Übersicht über den vollen Funktionsumfang bietet die Homepage von Scilab, eine deutschsprachige Einführung gibt es ebenfalls.
Verwendung von Scilab in der Graphentheorie
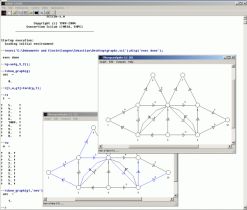
In Scilab werden Graphen in der Graphlist-Datenstruktur abgebildet. Die Bearbeitung der Graphen kann direkt in der Scilab-Konsole vorgenommen werden. Hierbei können die Befehle der MetaNet-Bibliothek genutzt werden oder direkt auf einzelne Elemente eines Graphen zugegriffen werden. Eine weitere Möglichkeit zur Darstellung und Bearbeitung eines Graphen bietet das MetaNet-Fenster, das aus der Konsole aufgerufen wird.
Für den Kurs 00852 »Optimierung in Graphen« wurden einige der in Kurseinheit 1 »Grundlagen der Graphentheorie« behandelten Algorithmen in Scilab implementiert. Zudem sind auch die verwendeten Graphen durch Befehle generierbar. Die Implementierung erfolgte in der Scilab-Skriptsprache und ist eng an die im Kurs dargestellte programmiernahe algorithmische Form angelehnt. Um die Algorithmen zu verwenden, muss die Datei scilab.zip (ZIP 8 KB) in das Programmverzeichnis kopiert und entpackt werden. Danach können die unten aufgeführten Beispiele zur Graphentheorie in Scilab über das Menü direkt aufgerufen werden. Die Datei readme.txt enthält eine entsprechende Anleitung.
Entwicklungen und Beispieldaten
| Algorithmus | Funktion | Eingabevariable | Ausgabevariable |
|---|---|---|---|
| Topologische Sortierung | g1=Top_sort(g); | g: scilab-Graph | g1: scilab-Graph, bei dem die Namen der Knoten, Nummern sind, so dass der Graph topologisch sortiert ist. |
| Minimalgerüst mit Primalgorithmus | g1=prim(g); | g: scilab-Graph | g1: scilab-Graph, bei dem das Minimalgerüst blau eingezeichnet ist. |
| Kürzeste Wege mit dem Algorithmus von Bellman | [l,w,g1]=bellman(g,a); | g: scilab-Graph a: Startknoten | l: Vektor der Weglängen w: Vektor mit direktem Vorgänger g1: scilab-Graph, bei dem die kürzesten Wege blau eingezeichnet sind. |
| Kürzeste Wege mit dem Algorithmus von Dijkstra | [l,w,g1]=dijkstra(g,a); | g: scilab-Graph a: Startknoten | l: Vektor der Weglängen w: Vektor mit direktem Vorgänger g1: scilab-Graph, bei dem die kürzesten Wege blau eingezeichnet sind. |
| Kürzeste Wege mit dem Algorithmus von Ford | [l,w,g1]=ford(g,a); | g: scilab-Graph a: Startknoten | l: Vektor der Weglängen w: Vektor mit direktem Vorgänger g1: scilab-Graph, bei dem die kürzesten Wege blau eingezeichnet sind. |
| Kürzeste Wege mit dem Tripel-Algorithmus | [g,d,q]=triple(g); | g: scilab-Graph | Matrizen q, d dem Kurs entsprechend |
Folgende Beispiele und Übungsaufgaben der Kurseinheit 1 wurden bereits implementiert und können direkt aufgerufen werden.
| Aufgabe | Seite | Funktion |
|---|---|---|
| Übungsaufgabe 1.14 | 26 | g=aufg_1_14(); |
| Beispiel 3.1 | 41f | g=bsp_3_1(); |
| Übungsaufgabe 3.2 | 46 | g=aufg_3_2(); |
| Beispiel 3.2 | 49 | g=bsp_3_2(); |
| Beispiel 3.3 | 53 | g=bsp_3_3(); |
| Übungsaufgabe 3.4 | 54 | g=aufg_3_4(); |
| Beispiel 3.4 | 58 | g=bsp_3_4(); |
| Beispiel 3.5 | 63 | g=bsp_3_5(); |
| Beispiel 3.6 | 65 | g=bsp_3_6(); |
| Übungsaufgabe 3.6 | 66 | g=aufg_3_6(); |


