List of References

We compiled a list of references and an author index which you can find in our bibliography (pdf-file). Comments, corrections and additions are welcome.

Graph Colouring Games

An introduction (by S.D. Andres)

Maker-breaker graph colouring games are non-cooperative games played by a maker, Alice, and a breaker, Bob. By certain rules, the players colour certain elements of the graph with a colour from a given colour set. Alice's goal is to achieve a graph where all considered elements of the graph are coloured. Bob tries to create a situation where some uncoloured elements cannot be coloured any more by the rules.

The most important parameter of this game is, for a graph G, the smallest number of colours, so that Alice has a winning strategy for the game. Usually, the rules are chosen in such a way that this parameter is well-defined. So, if this parameter is k, then Bob wins for all games with fewer than k colours on G. However, for some games it is not clear whether, if Alice wins on G with k colours, Alice wins on G with more than k colours.

There are various types of this game. The most important and oldest one is the vertex colouring game of an undirected graph. It was proposed by Brams in 1981 and reinvented by Bodlaender in 1991. Here, Alice and Bob alternately colour vertices of the graph, so that adjacent vertices receive distinct colours. The game ends if either all vertices are coloured (in which case Alice wins) or if there is an uncoloured vertex surrounded by vertices of all colours. The parameter defined by this game is called game chromatic number of the graph. The study of the game chromatic number for special classes of graphs was initiated by the work of Faigle et al. (1993). Obviously, the game chromatic number is a competitive version and an upper bound of the chromatic number of a graph.

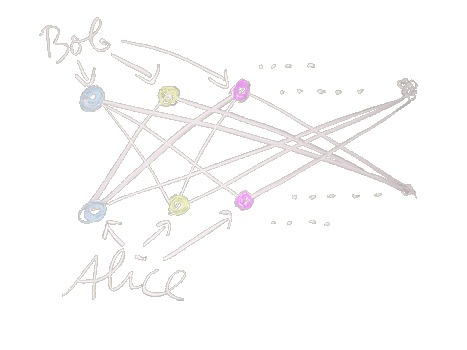
In the game defining the game chromatic number, Alice has the first move. The game where Bob has the first move may define a completely different parameter. Consider the complete bipartite graph with 2n vertices and delete a perfect matching in it (see figure above). The resulting graph has game chromatic number n (Bob may play according to a copycat strategy) but the parameter for the game where Bob has the first move is only 2. The same example can be used to show that, in general, the game chromatic number of a subgraph H of a graph G is not necessarily smaller or equal to the game chromatic number of G. This is an example of Kierstead.

We will now list some other variants of games.

The edge colouring game

Here edges of a graph are coloured instead of vertices. The parameter defined hereby, the game chromatic index, is a game-theoretic analogon of the chromatic index. The edge colouring game was introduced by Cai and Zhu. It is the special case of the vertex colouring game for line graphs.

The incidence colouring game

Here incidences of a graph are coloured instead of vertices. The parameter defined hereby, the incidence game chromatic number, is a game-theoretic analogon of the incidence colouring number. This game was introduced by me. It is the special case of the vertex colouring game for incidence graphs. (You might also be interested in The Incidence Coloring Page maintained by Eric Sopena.)

Digraph colouring games

Here vertices of a digraph are coloured in such a way that an uncoloured vertex may not receive the colour of any of its in-neighbours. The parameter defined hereby, also called game chromatic number, is a game-theoretic analogon of the dichromatic number. Digraph colouring games were introduced by me. The vertex colouring game of a graph is a special case of these games since a graph is a digraph with pairs of antiparallel arcs.

Asymmetric graph colouring games

Here, Alice and Bob do not necessarily colour one vertex in a move, but there are numbers a and b, so that Alice colours a and Bob colours b vertices in a move. These games were introduced by Kierstead.

Marking games

For all the afore-mentioned games one may define marking games. The parameter defined by the marking game associated with the ordinary colouring game is a game-theoretic analogon of the colouring number, and is called game colouring number. It was introduced by Zhu.

Relaxed graph colouring games

Here, vertices may have up to a certain number of neighbours with the same colour. The parameters defined hereby are competitive versions of relaxed graph colouring parameters. Relaxed graph colouring games were introduced by Chou et al.

The new game chromatic number

Here, Bob may not use a colour that has not been used before, except if he is forced to do so. The parameter new game chromatic number was introduced by Chen et al.

The oriented game chromatic number

This parameter is a game-theoretic analogon of the oriented chromatic number of an oriented graph. It was introduced by Nešetřil and Sopena.

Combinations

Combinations of these games were considered, too.